Reiknitorg * Til baka í efnisyfirlit algebru Óla Dan
Algebra - Æfingar XIV - svör
Rætur, brot, annars stigs jöfnur
Sendu mér póst ef þú
finnur villur!

Ath. Þegar almennt brot hefur verið lengt þannig að talan í nefnara verður skráð með aðeins tölustafnum 9 þá er teljari bortsins umferðin, þ.e. lota lotubundna tugabrotsins.
a) 1/11 = 09/99 =
0,0909090909 ...
- umferðin er 09
b) 6/7 = 0,85714285714285 ...
- umferðin er 714285
c) 11/13 = 846153/999999 = 0,846153846153 ...
- umferðin er 846153
d) 37/41 = 0,9024390243 ...
- umferðin er 90243
e) 15/44 = 0,34090909 ...
- umferðin er 09
f) 53/74 = 0,7162162 ...
- umferðin er 162
a) 0,72727272 ... = 72/99 = 8/11
b) 0,729729729 ... = 729/999 = 27/37
c) 0,0627306273 ... = 06273/99999 = 17/271
d) 0,2777777777 ... = 2/10 + 7/90 = 5/18
e) 0,261363636 ... = 261/1000 + 36/99000 = 23/88
5.
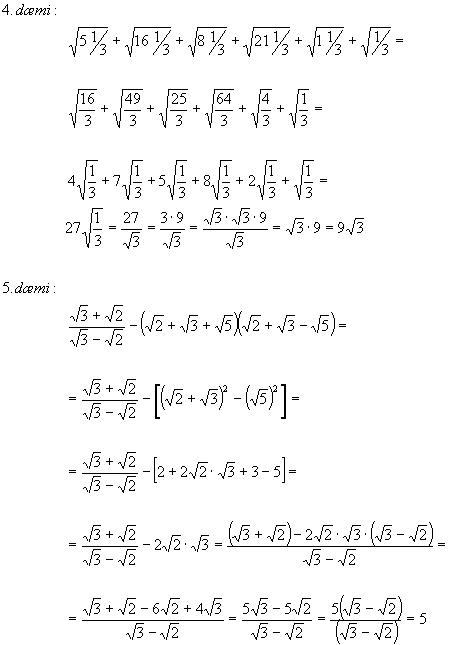
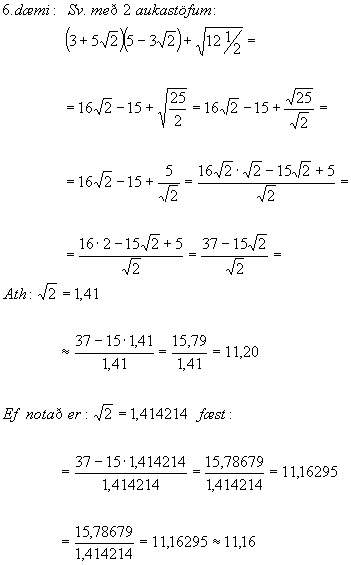
8.
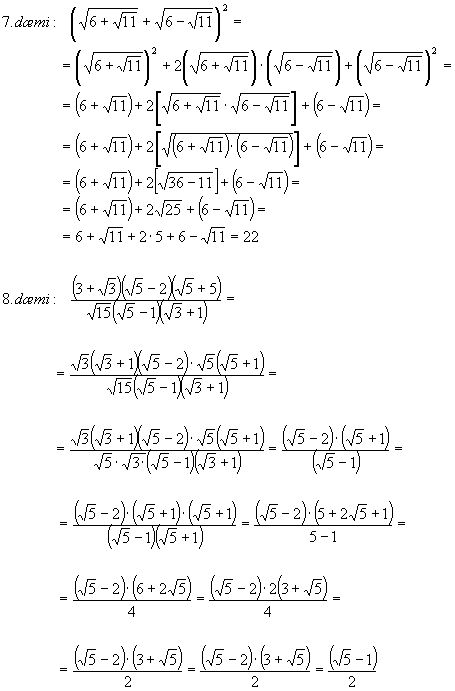


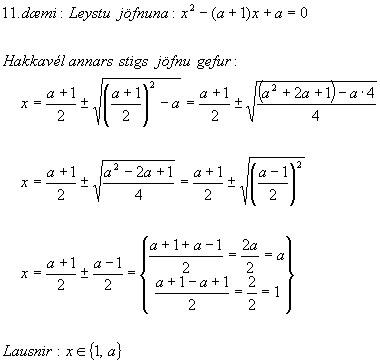
Lausn:
Breiddin er x og lengdin er x+3.
* *
x.(x+3)=378 sem gefur annars stigs jöfnuna
x2 +3x-378=0 sem gefur lausnirnar x = 18 og x = - 21 sem er
ónothæf lausn.
x = 18 er nothæf lausn og er breiddin í metrum.
Lengdin er x + 3 = 18 + 3 = 21 m.
Lausn: Straumhraði fljótsins er 6 km/klst.
* *
Straumhraði fljótsins er x km/klst.
Hraði bátsins upp eftir fljótinu er (18 - x) km/klst.
Hraði hans niður fljótið er (18 + x) km/klst.
Ferðin upp fljótið tekur hann 9/(18-x) klst og
ferðin niður fljótið tekur 9/(18+x) klst sem samtals er 67,5/60 = 9/8 klst
Þetta er jafnan:
9/(18-x) + 9/(18+x) = 9/8
Lagfærð verður annars stigs jafnan: x2 = 36 þar sem nothæfa lausnin er x = 6.
Lausn: Tölurnar eru 3, 4 og 5 eða -1, 0, 1.
* *
Tölurnar eru x og (x+1) og (x+2) og orðalagið segir
(x+2)2 = x2 + (x+1)2 sem lagfært verður:
x2 - 2x - 3 = 0 með lausnunum x = -1 og x = 3 sem báðar eru
nothæfar.
Lausn:
Lengdin er x og breiddin er 270/x
* *
Að viðbættum gangstígnum er flatarmálið 340 m2
Lengd blettsins að viðbættum gangstígnum beggja megin er x + 2 og breiddin
verður á sama hátt (270/x + 2) og flatarmálið samanlagt fæst þá úr
jöfnunni:
(x + 2).(270/x + 2) = 340
Annars stigs jafnan verður x2 - 33x + 270 = 0
og lausnirnar verða x = 18 og x = 15.
Ef x = 18 verður 270/x = 15 og öfugt.
Niðurstaðan er þessi: Önnur hliðin er 15 m og hin er 18 m.
Lausn: Bræðurnir voru 7
* *
Bræðurnir eru x
Systurnar eru (11-x)
Hver systirin fær 3000 krónum meira en hver bræðranna.
Ef við drögum samanlagða þá upphæð frá upphæð arfsins verða
eftir
(56000 - (11-x)*3000) = (23000 + 3000x) kr og þær skiptast jafnt milli
allra.
Hvert systkinanna fær þá (23000 + 3000x)/11 en hver systranna 3000 kr að
auki. Til samans fá bræðurnir jafn mikið og systurnar - sem merkir að:
x*(23000 + 3000x)/11 = (11-x)*(23000 + 3000x)/11 + (11-x)*3000
Löguð til verður jafnan þannig:
3x2 + 23x - 308 = 0 sem gefur eina nothæfa lausn: x = 7
Lausn: 25 kökur.
* *
Kökurnar eru x
Hver kaka kostaði 100/x
Kökurnar nýttust honum þannig:
Hann borðaði sjálfur 3 fyrir 3 * 100/x aura
Hann seldi samtals (x-3) fyrir alls (x-3) * (100/x + 1) og hafði þá grætt
10 aura.
Jafnan verður svona:
3 * 100/x + (x-3) * (100/x + 1) = 110
Lagfærð verður jafnan:
x2 - 13x - 300 = 0 með lausnunum x = 25 og einnig ónothæfa
lausnin x = -12.
Lausn:
10 sm.
* *
Breidd rammans er x sm.
Flatarmál myndarinnar er 2400 sm2
Samanlögð lengd rammans er 2 * 60 + 2 * 40 + (fjögur horn = 4*x)
Flatarmál rammans er því:
x * ( 2 * 60 + 2 * 40 + 4x) = 2400
Lagfærð verður jafnan þannig:
x2 + 50x - 600 = 0 sem gefur eina nothæfa lausn: x = 10
Lausn: 30 aura.
* *
Eggið kostar x aura.
Ef tylftin hækkar um 40 aura hækkar hvert egg um 40/12 = 10/3 aura.
Fyrir 300 aura fást núna 300/x egg
Eftir hækkun fengjust 300/(x + 10/3) egg en það er 1 færra.
Jafnan er því:
300/x = 300/(x + 10/3) + 1
sem lagfærð verður þannig:
x2 + 10/3 * x - 1000 = 0 sem gefur eina nothæfa lausn: x =
30
Lausn: 3,5 m.
* *
Hann bað um x m.
Hann ætlaði að greiða kr. 68,25/x fyrir hvern metra.
Hann greiddi í raun kr. (68,25/x + 1,50) fyrir hvern metra og hann
keypti í raun (x - 1/4) m en samt greiddi hann sömu upphæð og hann hafði
ætlað sér. Jafnan er því þessi:
(x - 1/4) * (68,25/x + 1,50) = 68,25
sem lagfært verður þannig:
x2 - 0,25 * x - 11,375 = 0 sem gefur eina nothæfa lausn: x = 3,5
(Prófdæmi í Akureyrarskóla 1925)
Lausn: Skipverjarnir hafa verið annað hvort 32 eða 40. Af
upplýsingunum í dæminu verður ekki sagt hvor talan það er.
* *
Skipverjar eru x
Hverjum voru ætlaðir 10/x pottar
Þeir heilbrigðu minnkuðu sinn skammt um 1/4 pela sem er 1/16 pottur.
Þá fékk hver hinna veiku viðbót sem dugði upp í 1/2 pott.
Þessi viðbót var (1/2 - 10/x) á hvern hinna veiku.
Öll minnkunin dugði fyrir allri aukningunni. Jafnan er svona:
(x-8)*(1/16) = 8 * (1/2 - 10/x)
sem lagast yfir í
x2 -72x + 1280 = 0 sem gefur tvær nothæfar lausnir: x = 32 og x =
40.
(Reikningsbók Eiríks Briem, síðari partur, 1880, önnur útgáfa, 8. d. á 82. bls).
Lausn: 90
* *
Alls snæða x félagsmenn og hver þeirra greiðir 441/x. Ef gestirnir hefðu
greitt sinn hlut hefði hveer veislugestur aðeins þurft að greiða 441/(x+8).
Sú upphæð hefði verið 0,40 lægri.
Þetta er jafnan:
441/x - 441/(x+8) = 0,40
Annars stigs jafnan verður svona:
x2 + 8x - 8820 = 0
Lausn: Annað hvort 25 km eða 30 km á klst.
* *
Upphafshraðinn er x km/klst og áætlunartíminn er 600/x klst.
Þegar hún stansar hefur hún ekið í 12 klst og á því eftir (600/x - 12)
klst af áætlunartímanum. Þá tefst hún um fjórðunginn af þessum tíma
eða um (150/x - 3) klst.
Þegar hún fer aftur af stað er hún búin að vera á leiðinni í:
12 + (150/x - 3) = (150/x + 9) klst alls. Hún á þá eftir af
áætlunartímanum:
600/x - (150/x + 9) = (450/x - 9) klst.
Þennan tíma ekur hún á (x + 5) km/klst.
Á áætlunartímanum kemst því svona langt:
12x + (450/x - 9)(x + 5) = 570
Þegar þú hefur einfaldað þessa jöfnu lítur hún svona út:
x2 - 55x + 750 = 0 sem gefur lausnirnar x = 25 og x = 30 og
þær koma báðar til greina. Hins vegar eru ekki í dæminu nægar
upplýsingar til að ákvarða hvor lausnin á frekar við.