GÓP-fréttir: Reiknitorg Vefskólans

Forsíða	Reiknitorg * Til baka í efnisyfirlit algebru Óla Dan Algebra - Æfing VIII Óuppsettar jöfnur Sendu mér póst ef þú finnur villur!
1.	Ég hugsa mér tölu, bæti við hana 1, deili í summuna með 4 og bæti 2 við kvótann. Þá er komin aftur talan sem ég hugsaði mér. Hver var hún? Lausn: Talan er x Orðalagið segir: (x + 1)/4 + 2 = x sem lagað verður: 3x = 9 sem gefur x = 3
2.	Ég hugsa mér tölu, þrefalda hana og bæti 7 við. Síðan deili ég 8 í það sem þá er komið út og bæti 1 við kvótann. Þá er komin talan sem ég hugsaði mér. Hver var hún? Lausn: Talan er x Orðalagið segir: (x^.3 + 7)/8 + 1 = x sem lagað verður: 5x = 15 sem gefur x = 3
3.	Ég hugsa mér tölu, þrefalda hana og dreg 8 frá. Síðan deili ég með 7 og bæti 4 við kvótann. Þá er komin út talan sem ég hugsaði mér. Hver var hún? Lausn: Talan er x Orðalagið segir: (3x - 8)/7 + 4 = x sem lagað verður: 4x = 20 sem gefur x = 5
4.	Ég hugsa mér tölu, tvöfalda hana og dreg 9 frá. Deili síðan því, sem þá er komið út, með 5 og bæti 2 ¹/₂ við kvótann. Þá er komin út tala sem er einum minni en helmingur þeirrar tölu sem ég hugsaði mér. Hver var hún? Lausn: Talan er x Orðalagið segir: (2x - 9)/5 + 2 ¹/₂ = x/2 - 1 sem lagað verður x = 17
5.	Ég hugsa mér tölu, hækka hana um 1 og þrefalda útkomuna. Síðan bæti ég aftur 1 við, og deili nú með 7 í það sem út er komið. Við kvótann bæti ég tvöfaldri upphaflegu tölunni og dreg svo 13 frá summunni. Talan sem þá kemur út er einum minni en sú sem ég hugsaði mér. Hver var hún? Lausn: Talan er x Orðalagið segir: [(x + 1)^.3 + 1]/7 + 2x - 13 = x - 1 sem lagað verður 10x = 80 sem gefur x = 8
6.	Ég hugsa mér tölu, dreg 5 frá henni, tvöfalda mismuninn og bæti einum við. Síðan deili ég með 13 í það sem út er komið og dreg 3 frá kvótanum. Þá er ekkert eftir. Hver var talan sem ég hugsaði mér? Lausn: Talan er x Orðalagið segir: [(x - 5)^.2 + 1]/13 -3 = 0 sem lagað verður 2x = 48 sem gefur x = 24
7.	Ég hugsa mér tölu, bæti við hana 1 og deili svo með 7. Síðan bæti ég 11 við kvótann, deili svo aftur með upphaflegu tölunni og dreg 1 frá útkomunni. Þá kemur út það sama sem komið hefði ef ég hefði deilt með upphaflegu tölunni í 19 ¹/₂ og dregið 1 ¹/₂ frá kvótanum. Hver var talan sem ég hugsaði mér? Lausn: Talan er x Orðalagið segir: [(x + 1)/7 + 11]/x -1 = (19 ¹/₂ )/x - 1 ¹/₂ sem lagað verður 9x = 117 sem gefur x = 13
8.	Maður nokkur hafði ákveðið svo í erfðaskrá sinni að kona hans skyldi hafa helming eigna hans, barn þeirra ¹/₃ en bróðir hans ¹/₁₂ og það sem þá var eftir, kr. 1.200, gaf hann til góðgerðarmála. Hve miklar voru eignir hans? Lausn: Eignirnar eru kr. x Orðalagið segir: x/2 + x/3 + x/12 + 1200 = x sem lagað verður: x = 14400
9.	Peningaupphæð var þannig skipt milli tveggja manna að annar fékk helminginn og 3 kr. að auki en hinn þriðjunginn og 13 kr. að auki. Hver var peningaupphæðin sem skipt var og hve mikið fékk hvor mannanna um sig? Lausn: Upphæðin er x Orðalagið segir: x = (x/2 +3) + (x/3 + 13) sem lagað verður x = 96 Sá fyrri fékk 96/2 + 3 = 51 Hinn fékk 96/3 + 13 = 45
10.	Maður nokkur tapaði í spilum helmingi þess er hann hafði á sér af peningum. Hann hélt nú um stund áfram og græddi þá 5 kr. Svo tapaði hann aftur helmingi þess sem hann nú hafði en græddi aftur 8 kr. Hann hafði þá jafnt og hann byrjaði með. Hve mikið var það? Lausn: Hann byrjaði með kr. x Orðalagið segir: (x/2 + 5)/2 + 8 = x sem lagað verður 3x = 42 sem gefur x = 14
11.	Maður nokkur átti 100 kr. í sparisjóði. Hann tók nú út nokkrar krónur og skömmu seinna tók hann helming þess sem eftir var og var það þrefalt við það sem hann hafði tekið fyrst og einni krónu betur. Hve mikið tók hann út í fyrra skiptið og hve mikið á hann nú eftir í sparisjóðnum? Lausn: Í fyrra skiptið tók hann út kr. x Orðalagið segir: Seinni úttektin er einni krónu hærri tala heldur en þreföld fyrri úttektin. Jafnan verður því svona: (100 - x)/2 = 3x + 1 sem lagað verður 7x = 98 sem gefur x = 14 Eftir báðar úttektirnar eru þá eftir kr. 100 - 14 - (100 - 14)/2 = 43
12.	A og B eiga að grafa skurð, 125 m að lengd. A grefur alltaf 6 m á dag. B grefur 5 ¹/₄ m fyrsta daginn, 5 ³/₄ m annan daginn en 6 m hvern dag eftir það - eins og A. Hve marga daga eru þeir með verkið? Lausn: Þeir eru x daga með verkið. A grefur 6x metra og B grefur 5 ¹/₄ m + 5 ³/₄ m + 6(x - 2) og saman grafa þeir allan skurðinn. Jafnan er því svona: 6x + [5 ¹/₄ + 5 ³/₄ + 6(x - 2)] = 125 sem lagað verður 12x = 126 sem gefur x = 10,5
13.	Árið 1907 var aldur minn ³/₄ af því sem hann var 1917. Hve gamall var ég 1927? Lausn: Aldur minn árið 1927 er x Aldurinn árið 1917 var (x - 10) Aldurinn árið 1927 var (x - 20) Ad orðalaginu fæst þessi jafna: (x - 20) = (x - 10)^. ³/₄ sem lagað verður x = 50
14.	Tveir menn tóku peninga úr sömu buddunni. Annar tók 2 kr. og sjötta hlutann af því sem eftir var. Hinn tók síðan 3 kr. og sjötta hlutann af því sem þá var eftir. Nú höfðu þeir tekið jafnt, Hve mikið var í buddunni í fyrstu? Lausn: Í buddunni voru upphaflega kr. x Orðalagið segir að það sem sá fyrri tók = það sem sá síðari tók og jafnan verður því: [2 + (x - 2)/6] = [3 + {x - 3 - [2 + (x - 2)/6]}/6] sem lagað verður x = 20
15.	Hvenær koma vísarnir á úrinu saman í fyrsta skipti eftir kl. 7? Lausn: Svar: Kl. 38 ²/₁₁ mínútur yfir 7. A: Stóri vísirinn hefur þá gengið x mínútur Litli vísirinn hefur gengið 12/x mínútur. Staða litla vísisins er þá á 35 + x sem er sama staða og þess stóra. Jafnan er því svona: 35 + x/12 = x sem lagað verður 11x = 420 sem gefur x = 38 ²/₁₁ B: Látum litla vísinn hafa gengið x mínútur. Þá er jafnan svona: 35 + x = 12x sem lagað verður 11x = 35 sem gefur x = 3²/₁₁ sem með 35 + 3²/₁₁ gefur ferðalag stóra vísisins = = 38 ²/₁₁ mínútur yfir 7. Kosturinn við B-aðferðina er sá að tölurnar eru lægri - en ókosturinn er sá að maður verður að muna í lok dæmisins að það var ekki spurt um ferðalag litla vísisins.
16.	Hvenær verða vísarnir á úrinu í beinu framhaldi hvor af öðrum í fyrsta skipti eftir kl. 7? Lausn: Kl. 5 ⁵/₁₁ mínútur yfir 7. Litli vísirinn hefur þá gengið x mínútur og er staddur á 35 + x Stóri vísirinn er genginn fram yfir 1 um x mínútur. Jafnan verður svona: Gangur stóra vísis = 5 + gangur litla vísis 12x = 5 + x sem lagað verður 11x = 5 og gefur x = 5/11 Klukkan er þá gengin 5 5/11 mínur í 8.
17.	Hvenær verður rétt horn á milli vísanna á úrinu í fyrsta skipti eftir kl. 7? Lausn: Kl. 21 ⁹/₁₁ mínútur yfir 7. Litli vísirinn er genginn x mínútur og er staddur á 35 + x Stóri vísirinn er genginn 12x mínútur og er staddur á 20 + x sem er jafnan: 12x = 20 + x sem lagað verður 11x = 20 og gefur x = 1 9/11 Klukkan er þá gengin 21 9/11 mínútur í 8.
18.	Hvenær verður litli vísirinn á úrinu mitt á milli stóra vísisins og 12 í fyrsta skipti eftir kl. 1? Lausn: Kl. 12 mínútur yfir 1. Þá hefur litli vísirinn gengið x mínútur og er staddur á 5 + x Stóri vísirinn hefur þá gengið 12x og er staddur á 10 + 2x sem er jafnan: 12x = 10 + 2x sem gefur x = 1 Klukkan er þá gengin 12 mínútur í 2.
19.	Hvað er klukkan langt gengin átta þegar stóri vísirinn er jafn miklu til hægri handar eins og litli vísirinn er til vinstri handar? Lausn: Kl. 23 ¹/₁₃ mínútur yfir 7. Litli vísirinn hefur gengið x mínútur og er staddur í 35 + x sem er 5 + x mínútum vinstra megin við töluna 6 á botni klukkuskífunnar. Stóri vísirinn er jafnlangt hægra megin og á því eftir 5 + x mínútar í að vera kominn að 6. Hann er því staddur í 30 - (5 + x) og jafnan verður svona: 12x = 30 - (5 + x) sem lagað verður 13 x = 25 sem gefur x = 1 12/13 Klukkan er þá gengin 30 - (5 + 1 12/13) = 23 1/13 mínútur í 8
20.	Hve langt er klukkan gengin 12 þegar stóri vísirinn er jafn miklu til hægri handar frá 12 eins og litli vísirinn er til vinstri handar? Lausn: Kl. 4 ⁸/₁₃ mínútur yfir 11.
21.	Nemandi átti að hafa í árskaup 120 kr. og eina flík. Eftir 5 mánuði var honum goldið kaupið fyrir þann tíma og fékk hann þá 36 kr. og flíkina. Hve mikils virði var hún talin? Lausn: Flíkin kostaði x Fimm tólftu árskaupsins = 36 + x sem er jafnan: 5(120 + x)/12 = 36 + x sem lagað verður 7x = 168 sem gefur x = 24
22.	Forngrikki fór í hof Seifs og bað guðinn að láta tvöfaldast þá peninga sem hann hafði á sér. Honum varð óðara að ósk sinni. Hann varð frá sér numinn af þakklæti og fórnaði guðinum 8 obólum. Þá gekk hann í hof Appollós og bað sömu bænar. Hann var bænheyrður og fórnaði jafn miklu og áður. Þaðan varð honum reikað í hof Aþenu og þar fór allt á sömu leið. Loks fór hann að gæta að því hve miklir peningarnir væru. Kom þá í ljós, honum til sárra vonbrigða, að hann var alveg peningalaus. Hve mikla peninga bar hann á sér þegar hann kom í hof Seifs? Lausn: Í upphafi hafði hann x obólur. Orðalag jöfunnar segir: Í síðasta hofinu, hofi Aþenu, hefur hann tvöfalt það sem hann kom með þangað og að frá dregnu 8 er það 0. En það sem hann kom með þangað var tvöfalt það sem hann hafði með sér í hof Appolós frádregnum 8 En það sem hann hafði með sér í hof Appolós var tvöfalt það sem kom með í hof Seifs að frádregnum 8. Jafnan verður því fyrsta setningin - þar sem hinar eru settar inn - svona: 2[2(2x - 8) - 8] - 8 = 0 sem lagað verður 8x = 56 sem gefur x = 7
23.	Þegar tölu nokkurri er deilt með 14 verður afgangurinn einn sautjándi hluti deilistofnsins en einum minni en heila talan í kvótanum. Hver er talan? Lausn: Talan er x Afgangurinn við deilinguna er ^x/₁₇ Textinn segir að heila talan í kvótanum sé einum hærri en afgangurinn- - þ.e. ( ^x/₁₇ + 1) Þegar deilt er í töluna með 14 kemur út heil tala og afgangur - sem einnig skal deila í með 14 - svona: ^x/₁₄ =( ^x/₁₇ + 1) + ( ^x/₁₇ )/₁₄ sem lagað verður 2x = 238 og gefur x = 119
24.	Hve mörgum lítrum af víni, sem kostar 78 aura hver lítri, þarf að blanda í 40 lítra, sem kosta 90 aura, til þess að græða 5 krónur á því að selja alla blönduna fyrir 85 aura lítrann? Lausn: Það þarf að blanda x lítrum af 78-aura víninu. 78x + 40 * 90 + 500 = (40 + x) * 85 sem lagað verður 7x = 700 sem gefur x = 100
25.	Sex stafa tala byrjar á 1. Sé sá stafur tekinn framan af tölunni og honum skeytt aftan við hana í staðinn verður talan þreföld við það sem hún var í upphafi. Hver er þessi tala? Lausn: Talan er x (x - 100000) * 10 + 1 = 3x sem lagast í 7x = 999999 sem gefur x = 142857
26.	Sex stafa tala byrjar á 4. Sé sá stafur tekinn framan af tölunni og honum skeytt aftan við hana í staðinn verður talan þriðjungi minni en hún var í upphafi. Hver er þessi tala? Lausn: Talan er x (x - 400000) * 10 + 4 = 2x/3 sem lagað verður 28/3 * x = 3999996 sem gefur x = 428571
27.	Hvaða tala er það sem verður 103 sinnum stærri en hún er, ef tölunni 93 er skeytt aftan við hana? Lausn: Talan er x x * 100 + 93 = 103x sem gefur x = 31
28.	Piltur nokkur gekk venjulega á hálftíma í skólann. Einu sinni á leiðinni þangað mætti hann kunningja sínum og tafðist í 7 mínútur. Þá er hann tók að nýju á rás, hljóp hann við fót. Var hann þá helmingi fljótari en áður. Þó kom hann tveim mínútum og seint í skólann. Hvar og hvenær tafðist hann? Lausn: Hann hafði gengið x mínútur þegar hann tafðist. Heildar ferðatíminn í skólann varð: x + 7 + (30 - x)/2 = 30 + 2 sem gefur x = 20 Þegar hann hafði gengið í 20 mínútur hafði lagt að baki 20/30 af leiðinni eða tvo þriðju leiðarinnar og átti þriðjung leiðar eftir.
29.	Innlánsvextir í banka eru 4 % en útlánsvextir 5 ¹/₂ %. Hve mörg % græðir bankinn á innlánsfé því, sem hann hefur veitt móttöku ef hann getur ekki lánað út af því nema 90 % ? Lausn: Í prósentum reiknast gróði hans eins og hann hefði fengið 100 kr. innlán. Hann lánar kr. 90 á 5,5% vöxtum og fær í vexti kr. 4,95 en verður að greiða 4% vext af 100 krónunum sem gerir 4 kr.. Mismunurinn er það sem hann heldur eftir: 4,95 - 4 = 0,95 af hverju hundraði sem jafngildir 0,95 %
30.	Kona nokkur selur helming eggja sinna og hálft egg í viðbót. Síðan selur hún helming þess sem þá er eftir og hálft egg í viðbót. Þannig heldur hún áfram að selja, alls fimm sinnum. Þá hefur hún selt öll eggin. Hve mörg egg átti hún upphaflega? Lausn: Konan átti x egg í upphafi. Við fylgjums með henni, athugum hvað hún selur mikið í hvert sinn og reiknum út hversu mikið hún á eftir þegar að næstu sölu kemur. Að lokinni síðustu sölunni vitum við að það sem þá er eftir er einmitt 0. Það gefur okkur færi á að reikna gildið á x.
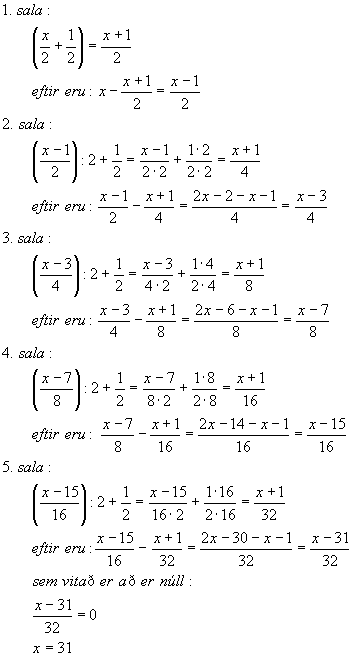
31.	Indverji lætur börnum sínum eftir í arf allmarga demanta, alla jafn verðmæta. Í erfðaskrá hans var svo fyrir mælt að elsta barnið skyldi fá 1 demant og 1/7 afgangsins, næstelsta barnið 2 demanta og 1/7 þess sem þá var eftir - og þannig skyldi haldið áfram að skipta. Við skiptin kom í ljós að börnin fengu jafnt. Hve mörg voru börnin og hve margir voru demantarnir? Lausn: Demantarnir eru x Öll börnin fá jafnt. Sá fyrsti fær jafnt og sá næsti sem ákvarðar jöfnuna: 1 + (x-1)/7 = 2 + {x - [1 + (x-1)/7] - 2}/7 sem lagað verður x = 36 demantar Reiknum hversu mikið elsta barnið fær: 1 + 35/7 = 6. Fjöldi barnanna er fjöldi demantanna /6 = 36/6 = 6 börn.

Efst á þessa síðu * Forsíða * Reiknitorg * Til baka í efnisyfirlit algebru Óla Dan