Forsíða

 

Bls:

Orðalisti

Blaðsíðutilvísun miðar við
Thomas' Calculus, 10th ed.
ISBN 0-201-44141-1

Yfirlit:
Bil = formengi
Continuity = samfelldni 
cosec og sec
samfelldni
sec og cosec

=> "Af því leiðir"
Rétt notkun: Sigga og Dúna eru alsystur og Jón er albróðir Siggu => Jón er albróðir Dúnu. 
= "er sama sem"
Sama-sem-merkið fullyrðir að sitt hvorum megin við það séu jafngildar stæður. 
Bil =
formengi		 Þegar fall er skilgreint fyrir tiltekin gildi á x og þau gildi eru samfelld á einhverju svæði er það svæði hér kallað bil og unnt er að sýna það með samfelldum línubúti á x-ásnum.
123 Continuity = samfelldni
Lýsing
í mæltu
máli		 Graf samfellds falls má draga með því að setja blýantinn á blaðið og draga - án þess að lyfta honum nokkru sinni upp fyrr en grafið hefur allt verið dregið. Grafið hangir alls staðar saman.
125 Samfelldni í punkti
Fall er samfellt í innri punktinum x = c á bili ef
sem merkir að
  • f(c) er til
  • f(x) hefur markgildi þegar x stefnir á c
  • og markgildi f(x) = f(c) hvort sem x nálgast c ofan eða neðan frá - þ.e. frá hægri eða vinstri..

Þessi þrjú atriði eru prófuð þegar kannað er hvort f(x) er samfellt í x = c.

Fall er skilgreint hægri- eða vinstri-samfellt í endapunkti þannig:

  • Hægri-samfellt fall í vinstri endapunkti bils er samfellt að endapunktinum frá hægri.
    Fall er skilgreint sem samfellt í vinstri endapunkti lokaða bilsins [a,b] - þ.e. í punktinum a, ef markgildi f(x) = f(a) þegar x nálgast a ofan = hægra-megin frá.
  • Vinstri-samfellt fall í hægri endapunkti bils er samfellt að endapunktinu frá vinstri.
    Fall er skilgreint sem samfellt í hægri endapunkti lokaða bilsins [a,b] - þ.e. í punktinum b, ef markgildi f(x) = f(b) þegar x nálgast b neðan = vinstra-megin frá.

Fall er samfellt í innri punkti bils ef það er bæði vinstri-samfellt og hægri-samfellt í þeim punkti.
Fall sem er samfellt í öllum innri punktum formengis síns - og í endapunktum ef bilið er lokað - er samfellt á því bili.

Ef f(x) er ekki samfellt í punktinum x = c er sagt að fallið sé ósamfellt í c og að c sé ósamfelldni-punktur fallsins. Vel getur verið að c sé ekki í formengi fallsins. Dæmi um slíkan ósamfelldnispunkt er þegar gildið x = c gerir nefnara ræðs falls að núlli.

Samandregið:
Fall er kallað samfellt þegar það er samfellt á því bili - eða á þeim bilum - þar sem það er skilgreint. Þetta orðalag gerir ekki kröfu til að aðskildir bútar fallsins á aðskildum bilum séu samfelldir. Ef bilin eru aðskilin þá er þar um að ræða ósamfelldnispunkt. Samfelldni er hugtak sem einungis er skilgreint á tilteknu bili og í punktum þess bils.

Lítum aðeins á fallið y = 1/x - sjá Ex.5 á bls 127:
Fallið er skilgreint á bilinu ]-oo,0[ ásamt ]0,oo[ og í öllum punktum hvors þessara bila uppfyllir það samfelldnisprófið.
Engu að síður er fallið ekki skilgreint í x = 0 og þess vegna er x = 0 ósamfelldnis-punktur og ósamfelldnin í þeim punkti er af tegundinni óendanleg ósamfelldni - sjá mynd 1.50c.

Þegar talað er um fallið y = 1/x er sjálfgefið að það er ekki verið að tala um það þegar x = 0. Þess vegna er til dæmis ekki unnt að tala um fallið á bilinu (-10,10). Sá sem ekki áttar sig á því verður að byrja á að setja niður fyrir sér hvert formengi fallsins er. Þegar það er klárt er jafnframt ljóst að fallið er samfellt á öllu fomenginu. Það er ekki unnt að finna neinn punkt í formenginu þar sem fallið er ekki samfellt. Það er hins vegar ekki samfellt frá öðru formenginu til hins og það er ekki heldur unnt að líma það saman með því að skilgreina y(0) - en það breytir engu um það að fallið er samfellt í öllum punktum formengisins.

Fall sem er samfellt á þeim bilum þar sem það er skilgreint kallast samfellt þótt graf þess sé í aðgreindum bútum frá bili til bils.
Nauðsynlegt er að hafa í minni skilgreiningu þess falls sem unnið er með hverju sinni svo ekki séu dregnar ályktanir yfir ósamfelldnis-punkta eða ósamfelldnis-bil.

cosec
og sec

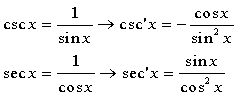
Um cosecant og secant.

Efst á þessa síðu * Forsíða