Forsíða

2.4-Leiðbeiningar og lasunir (5.12.2001)

Dæmasafn á bls. 184:
Dæmi: 1, 2, 8, 9, 11, 12, 13.

1. - 26.
dæmi:		 Reiknaðu afleiðuna.
5. dæmi: Diffra skal fallið y = (secx + tanx)(secx - tanx)

Lausn:
Unnt er að diffra margfeldið með aðferðinni (uv)' = u'v + uv' en ef ætlunin er að skila svarinu sem einföldustu kostar það töluverðar uppskriftir og nákvæmni í algebrunni. Önnur leið er að reyna að einfalda stæðuna áður en diffrað er. Hér verður byrjað á að margfalda svigana saman enda eru þeir af gerðinni (a + b)(a - b) = a2 - b2 og þá fæst:

y = sec2x - tan2x =



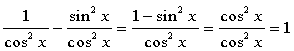
Í ljós kemur að y = 1 og þess vegna er y' = 0.

25. dæmi: Reikna skal y'' þegar y = csc x

Lausn - reiknuð með því að breyta csc x í 1/sin x:
y' = -csc x cot x = - (cos x) / (sin x)2 = - (cos x) (sin x)-2
y'' = -[-sin x sin-2x + cos x (-2sin-3x cos x)] = sin-1x + 2 cos2 sin-3x
= sin-1x + 2 (1- sin2) sin-3x = sin-1x + 2 sin-3x - 2sin-1x
= 2 sin-3x - sin-1x = 2 csc3x - csc x

27. - 30.
dæmi:		 Teiknaðu graf fallsins á bilinu sem tiltekið er. Teiknaðu snertla í þeim punktum sem tilteknir eru og tengdu jöfnur ferla og snertla við viðeigandi feril og snertil.
31. - 34.
dæmi:		 Reiknaðu hvort - og þá hvar graf ferilsins hefur lárétta snertla á bilinu [0, 2pí]. Ef enginn láréttur snertill er til skaltu útskýra hvers vegna svo er.
34. dæmi: Fallið er y = x + 2 cos x
(sem einnig mætti skrifa svona: y = x + cos x + cos x)

Lausn:
Láréttur snertill hefur hallatöluna núll.
Við reiknum afleiðuna:
y' = 1 - 2 sin x

Ef til er eitthvert x-gildi þar sem hallatala snertils er núll þá gildir þar að:

y' = 1 - 2 sin x = 0 eða styttra:
1 - 2 sin x = 0 sem við leysum með tilliti til sin x og fáum:

sinx = ½ sem gefur x = arcsin( ½ )

Öll x sem eru þannig að sin x = ½ eru lausn á þessari jöfnu en þar sem tekið er fram að lausnin skuli vera á bilinu [0,2pí] takmarkast lausnirnar við þau x sem eru þannig að sin x = ½ og x er á bilinu [0,2pí]

Taflan á bls. 46 segir okkur að þegar sin x = ½ er x = pí/6 og þá vitum við líka - með því að skoða einingarhringinn - að sin(5pí/6) = ½ og að ekki er um fleiri lausnir að ræða á hinu tiltekna formengi - þ.e. bilinu [0,2pí].

35. dæmi: Reiknaðu alla punkta á ferli fallsins y = tan x á bilinu á bilinu ]-pí/2, pí/2[ þar sem snertill til grafsins er samsíða línunni y = 2x. Teiknaðu grafið og snertilinn - eða snertlana - og tengdu saman hvern snertil og jöfnu hans og einnig graf fallsins og jöfnu þess.

Lausn:
Ef til er punktur á ferlinu þar sem snertillinn er samsíða línunni y = 2x sem merkir að snertillinn þarf að hafa hallatöluna 2, þá er afleiða fallsins í þeim punkti jöfn 2.

Reiknum afleiðuna:
f'(x) = 1/cos2x og ef eitthvert x-gildi er til þar sem f'(x) = 2 þá gildir þar að:
1/cos2x = 2 sem við leysum með því að umrita jöfnuna fyrst svona:

cos2x = ½ sem merkir að cos x = 1/(rótin af 2) eða x = -1/(rótin af 2)

Taflan á bls. 46 segir okkur að þau x-gildi á bilinu ]-pí/2, pí/2[ sem eru þannig að cos x = 1/(rótin af 2) séu aðeins tvö - þ.e. - pí/4 og +pí/4.

Skoðum fyrri punktinn:
x = -pí/4 og f(x) = f(-pí/4) = tan(-pí/4) = - 1
Punkturinn hefur hnitin (- pí/4 , - 1)
Snertillinn í þeim punkti hefur hallatöluna 2 og jafna hans er þá:
(y + 1) = 2 (x + pí/4) sem umrita má í y = 2x - 1 + pí/2

og snertillinn í hinum punktinum: (pí/4 , 1) og jafna hans er:
(y - 1) = 2 (x - pí/4) sem umrita má í y = 2x - 1 - pí/2

36. dæmi: Reiknaðu alla punkta á ferli fallsins y = cot x á bilinu á bilinu ]0, pí[ þar sem snertill til grafsins er samsíða línunni y = -x. Teiknaðu grafið og snertilinn - eða snertlana - og tengdu saman hvern snertil og jöfnu hans og einnig graf fallsins og jöfnu þess.
37. - 38.
dæmi:		 Reiknaðu jöfnur snertlanna sem teiknaðir eru rauðir inn á myndina í punktunum P og Q. Í punktinum Q er láréttur snertill.
37. dæmi: Fallið er f(x) = 4 + cot(x) - 2/sin(x)
Reikna skal jöfnu snertils í punktinum P(pí/2 ; 2) og punktinu Q en í honum er snertillinn láréttur.

Lausn:
Reiknum afleiðuna f'(x) = - 1/sin2x + 2cos x/ sin2x
sem umritast þannig í:

f'(x) = - (1/ sin2x)(1 - 2cosx)

Fyrst leitum við að jöfnu snertils í punktinum Q.
Sá snertill er láréttur. Það merkir að hallatala hans er núll. Það merkir að þar er f'(x) = 0 þ.e.:

- (1/ sin2x)(1 - 2cosx) = 0

Þetta er margfeldi tveggja þátta og við vitum að margfeldi verður aldrei núll nema einhver þáttanna sé núll. Við sjáum að fremri sviginn getur aldrei orðið núll. Einungis seinni sviginn getur orðið núll og það gerist þegar:

1 - 2cosx = 0

eða cos x = 1/2 sem gefa x = arccos(½) = pí/3.

Hnit punktsins Q eru því: (pí/3 , f(pí/3))
Reiknum f(pí/3):



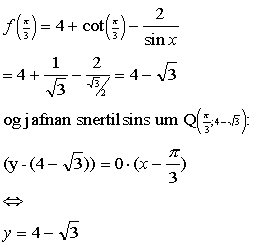
Næst leitum við að jöfnu snertils í punktinum P(pí/2 ; 2)

Hallatala snertilsins er:

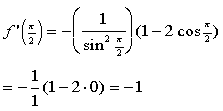
Jafna snertilsins er því:(y - 2) = - 1(x - pí/2)
sem jafngildir: y = -x + 2 + pí/2.

39. - 40.
dæmi:		 Jafnan gefur stöðu hlutar - þ.e. s = f(t) með s í metrum og t í sekúndum, þegar hann fer eftir s - ásnum. Reiknaðu afleiðu hlutarins, hraða hans og hröðun og líka hröðunarbreytinguna þegar t = pí/4 sek.
41. dæmi: Reiknaðu hvort til er gildi á c sem gerir fallið f(x) samfellt í s = 0.
42. dæmi: Reiknaðu hvort til er gildi á b þannig að fallið g(x) verði samfellt í x = 0. Gerir það gildi fallið afleiðanlegt í x = 0? Hvers vegna? - eða hvers vegna ekki?
43. dæmi: Reiknaðu y(999) af fallinu y = cos x.
44. dæmi: Reiknaðu afleiðureglur fyrir föllin y = tan x og y = cot x.

Efst á þessa síðu * Forsíða