Forsíða
|
1.2-Leiðbeiningar og lausnir (30.11.2001)
Dæmasafn á bls. 108:
Dæmi: 11, 13, 14, 15, 28 |
1. - 6.
dæmi: |
Notaðu grafið og segðu til um markgildin. |
7. - 8.
dæmi: |
Gerum ráð fyrir að markgildin þegar x -> 0 séu
fyrir f(x) = 1 og fyrir g(x) = -5.
Segðu til um hvaða markgildis-regla er notuð til að reikna frá
upphafsstöðunni í (a) og þaðan í (b) og svo í (c). |
| 9. dæmi: |
Gerum ráð fyrir að markgildin þegar x -> c séu
fyrir f(x) = 5 og fyrir g(x) = -2.
Reiknaðu markgildin. |
10.
dæmi: |
Gerum ráð fyrir að markgildin þegar x -> 4 séu
fyrir f(x) = 0 og fyrir g(x) = -3.
Reiknaðu markgildin. |
11. - 14.
dæmi: |
Reiknaðu markgildin. |
| 14. dæmi: |
c-liður:
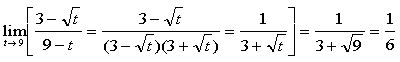 |
| 15. dæmi: |
a) Hægt er að sýna fram á (sanna) að ójafnan sé
rétt fyrir öll gildi á x í námunda við núll. Hvaða ályktun má af
því draga um markgildið?
Lausn - markgildið reiknað með pressu-aðferðinni -
og einnig með beint: Word-skjal
b) Rissaðu gröf fallanna þriggja og segðu hvað einkennir þau
þegar x stefnir á núll. |
| 16. dæmi: |
a) Hægt er að sýna fram á (sanna) að ójafnan gildi
fyrir öll gildi á x í námunda við núll. Hvaða ályktun má af því
draga um markgildið?
b) Rissaðu gröf fallanna þriggja og segðu hvað einkennir þau
þegar x stefnir á núll. |
17. - 20.
dæmi: |
Reiknaðu markgildin í x = xo + h þegar h
stefnir á núll. |
21.
dæmi: |
Hver þessara fullyrðinga um fallið f(x) á grafinu
eru réttar og hverjar eru rangar? |
22.
dæmi: |
Tiltekið er fallið f(x) og graf þess sýnt.
a) Reiknaðu markgildin þegar x -> 2+ og þegar x -> 2-.
b) Er limx->2 f(x) til? Já eða nei - hver eru rökin?
c) og d) Athugaðu hið sama þegar x -> 4. |
23. - 24.
dæmi: |
Athugaðu hvort vinstra markgildi og hægra markgildi
eru til og dragðu þar af ályktun um það hvort til er markgildi þegar
x -> 0. |
25. - 26.
dæmi: |
a) Hvert er formengi fallsins og hvert er varpmengið?
b) Hvaða x-gildi (x = c) er þannig að þar er til markgildið limx->c
f(x) ?
c) Hvar er aðeins til vinstra markgildi?
d) Hvar er aðeins til hægra markgildi? |
27. - 32.
dæmi: |
Reiknaðu markgildið. |
33.
dæmi: |
Skrifaðu upp misjöfnurnar og formengin.
Hvar í formenginu (fyrir hvaða c) ertu í fljótu bragði viss um að
til er limx->c f(x) ? Hver eru þessi markgildi? |
34.
dæmi: |
Gerum ráð fyrir að ójafnan gildi þegar x er ekki
2. Er af því unnt að draga einhverja ályktun um gildin á f og g og h
í x=2 ? Gæti f(2) verið núll? Gæti limx->2 f(x) = 0 ?
Rökstyddu svarið. |
35. - 36.
dæmi: |
Upp er gefin jafna sem þú notar til að reikna
markgildið. |
37.
dæmi: |
Gerum ráð fyrir að þú þekkir vinstra markgildi
að f(a) og hægra markgildi að f(a). Er það nóg fyrir þig til að
vita limx->a f(x) ? |
38.
dæmi: |
Ef þú veist að til er limx->c f(x) =
L
- er þá nóg fyrir þig að reikna hægra markgildið til að finna L ?
Já eða nei - hvers vegna? |