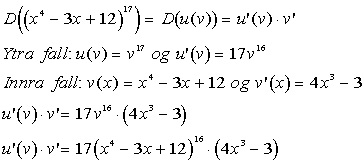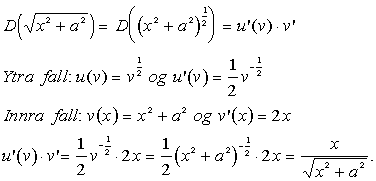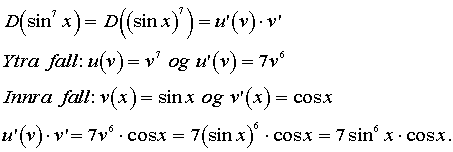Forsíða

Sjá
dæmi

Keðjureglan

Ef föllin f og g eru ræð og afleiðanleg (=diffranleg) föll gildir um samsetta fallið
y = f(g(x))
að afleiða þess er: y' = f'(g(x)) * g'(x)
f
og
g
eru
samfelld
ræð
föll

- -

 Athugaðu að ef t = x + h gildir:
h = t - x
limh->0 t = x og limh->0 g(t) = g(x)

Við gerum ráð fyrir að um x sé bil af að minnsta kosti lengdinni h í báðar áttir - þegar h er hæfilega lítil stærð en þó stærri en núll. Með öðrum orðum: x er innri punktur bils.

Afleiðan reiknast þannig:
Stytt-
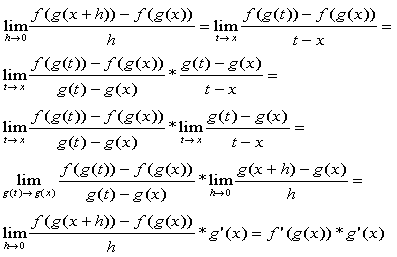
ing:		 Með því að rita u = f(x) og v = g(x) og f(g(x)) = u(v) verður keðjureglan einfaldari útlits þannig:

D(u(v)) = u'(v) . v'
Dæmi A:
Dæmi B:
Dæmi C:

Efst á þessa síðu * Forsíða|