Forsíða

Pyþagoras útvíkkaður

Samband hliðarlengda og horna í þríhyrningum:
c2 = a2 + b2 - 2ab cosC 

Þegar
pi/2 < v

þ.e.
hornið
v er
gleitt
horn

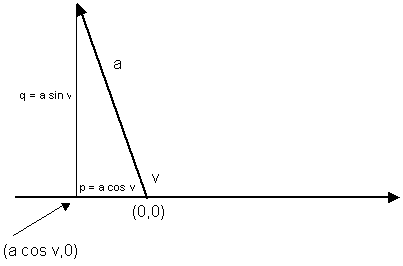
p/a = cos v
margföldum beggja megin með a og fáum:
p = a.cos v
Athugaðu að stærðin a.cos v er negatíf !!

q/a = sin v
q = a.sin v

Gleið-
hyrndir
þríhyrn-
ingar		 Útvíkkuð Pyþagorasar-regla er þessi:
Ef C er eitt horn í þríhyrningi, a og b eru aðlægar hliðar og c er mótlæg hlið þá gildir:
c2 = a2 + b2 - 2ab cosC 

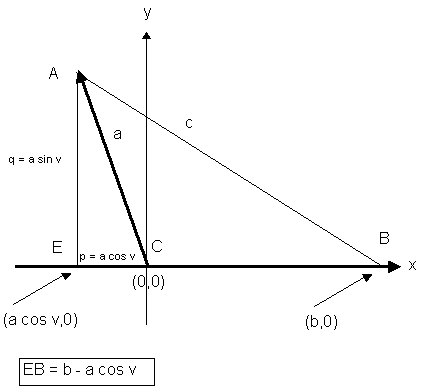
Þríhyrningurinn ABE er rétthyrndur.
Notum Pythagorasar-reglu:
AB2  = EA2  + EB2 

Setjum inn stærðirnar á myndinni og athugum að stærðin a cosC er negatíf:
c2 =  (a sinC)2 + (b - a cosC)2   

Reiknum út hægri hliðina:
c2 = a2 cos2C - 2ab cosC + a2 sin2C + b2  
sem umritast í:
c2 = (a2 cos2C + a2 sin2C)  - 2ab cosC + b2 
og áfram í:
c2 = a2 (cos2C + sin2C) + b2 - 2ab cosC
c2 = a2 + b2 - 2ab cosC

Niðurstaðan er þá sú að um alla gleið-hyrnda þríhyrninga gildir hin útvíkkaða Pyþagorasarregla:

c2 = a2 + b2 - 2ab cosC 

Hvass-
hyrndir
þríhyrn-
ingar

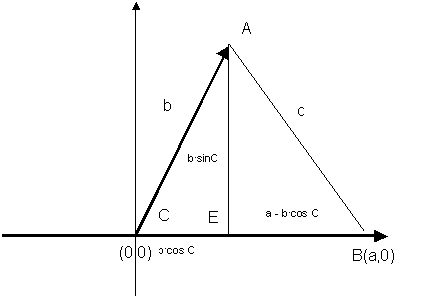
Pyþagorasar-regla á þríhyrninginn ABE skilar jöfnunni:
c2 = (a - b.cosC)2 + (b.sinC)2  
c2 = a2 + b2 .cos2 C - 2ab.cosC+ b2 .sin2 C  
c2 = a2 + b2 (cos2 C + sin2 C)  - 2ab.cosC
c2 = a2 + b2  - 2ab.cosC

Niðurstaðan er þá sú að um alla (gleið-hyrnda og hvass-hyrnda) þríhyrninga gildir hin útvíkkaða Pyþagorasarregla:

c2 = a2 + b2 - 2ab cosC 

Efst á þessa síðu * Forsíða